| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- coating
- Automotive
- oxygen vacancy
- EV
- ASSB
- ni-paste
- Murata
- dispersion
- mlcc
- ZrO2
- nickel
- microstructure
- BaTiO3
- hydrothermal
- halt
- CERAMIC
- X8R
- reliability
- X7T
- core-shell
- nano powder
- Powder
- CSZT
- NI-MLCC
- bme
- Barium titanate
- Zirconia
- C0G
- Sintering
- paste
- Today
- Total
MLCC Material & Process
제3장3절 MLCC의 각종 전기적 특성 본문
제3장 유전체 재료와 MLCC 특성
제3절 MLCC의 각종 전기적 특성 -현상론적 열역학을 이용한 특성 시뮬레이션
1. 서론
휴대전화, 모바일 컴퓨터로 대표되는 정보전자기기의 소형화, 고성능화, 전력절약화의 흐름은 멈출 줄 모르고, 이에 탑재되는 수동소자도 표면실장 가능한 칩화가 급속히 진전되고 있다. 가장 앞선 적층 수동 소자의 대표는 MLCC이다. MLCC의 기본 조성은 BaTiO3이며 1940대 초반에 미·일·소에서 발견되었으며, 이후 압전성, 강유전성, 구조 변화가 널리 연구되었으며 1949년 Kay and Vousden에 의해 그림 1에 나타낸 BaTiO3의 구조 변화가 보고되었다. BaTiO3의 강유전성이 발견된 것과 같은 무렵 오늘날 개인용 컴퓨터의 기초인 디지털형 컴퓨터 ENIAC가 개발되어 이후 저렴한 가격의 소형화·고성능화는 괄목할 만하다. 본 절에서는 간편하고 저렴한 개인용 컴퓨터(PC9801~)를 이용하여 BaTiO3의 현상론을 실제로 계산한 결과(1991년~)를 기술한다.
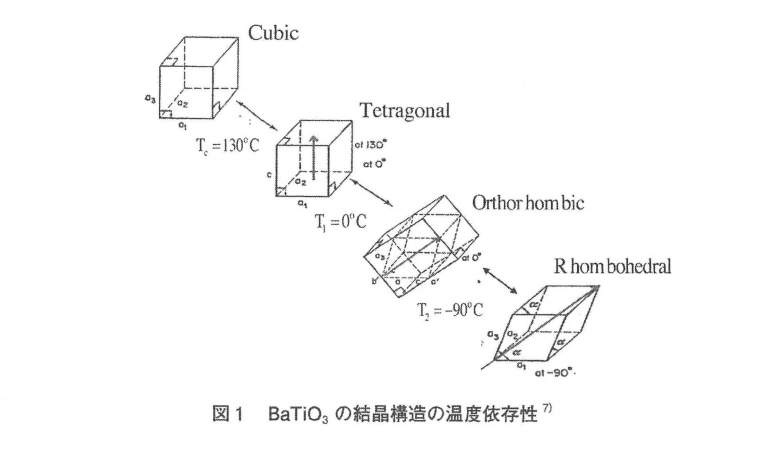
2. 현상론적 열역학에 의한 BaTiO3의 특성 시뮬레이션
1949년 Devonshire는 "티탄산 바륨의 이론"에서 깁스의 자유에너지 ΔG를 자발분극(Ps)으로 다음 식(1.1)과 같이 전개하여, 온도변화에 따른 결정구조 변화, 이어서 자발분극(Pi), 비유전율(εij), 격자상수(a, b, c)의 온도(결정구조) 의존성을 계산할 수 있음을 보여주었다. 이 논문이 강유전체 이론(현상론)의 시작이다. Dwonshire가 BaTiO3의 현상론 계산에 이용한 계수 파라미터는 Kay and Vousden에 의한 BaTiO3의 실험에서 얻은 파라미터일 것이다.

식(1.1)은 P1, P2, P3에 대해 대칭이며, 서로 교환해도 식의 형태는 변하지 않는다. 또, Pi의 짝함수로 되어 있어, P1과 Pi에 대해 같은 값을 부여한다. 때문에, 이 식은 페로브스카이트형 결정 구조의 대칭성(m3m)을 반영한다. 그림 1과 같이 저온 쪽에서 바라보면 능면 체정에서 사방정으로의 전이점(T2)은 약 -90℃, 사방정에서 정사각정으로의 전이점(T1)은 약 0℃이고, 정사각정에서 입방정으로의 전이점(T0)은 약 120℃이다. 온도변화에 따른 상변태(안정상과 상변태온도)를 계산하려면 먼저 표1에서 부여한 식(1.1)의 계수 파라미터를 부여하는 것이 필요하지만, 이 계수 파라미터를 결정하는 것은 쉽지 않다. 예로부터 여러 종류의 값이 보고되었다. 우선 자유에너지 ΔG의 식에 포함되는 계수 중 a12, a112, a123은 상수이며, 즉 온도 의존성이 없고, 정방정 이외의 자유에너지 ΔG에 포함된다. a112는 능면체정과 사방정에 포함되어 있으며, a123은 능면체정에만 포함된다.
먼저 a112를 변화시켜 사방정에서 정방정의 전이점(T1)을 결정하였다. 다음으로 a123을 변화시켜 능면체정에서 사방정의 전이점(T2)을 결정하였다. 자유 에너지 ΔG에서는 식(1.1)의 제1항에 포함되는 a1이 자유 에너지 ΔG의 크기, 특히 비유전율(εij)에 큰 영향을 준다. 비유전율 실험 결과에 맞도록 계수 a1이 정해졌다. 이상을 고려하여 결정한 계수를 표1에 나타내었다.

이러한 값을 이용하여 계산한 자유 에너지 ΔG의 온도 특성을 그림 2와 같다. T2=-65℃, T1=9℃이고 T0=113℃였다. T0~T1의 온도범위에서는 정방정이 안정, T1~T2 온도범위에서는 사방정이 안정, T2이하에서는 능면체정이 안정하다. (모두 자유에너지 ΔG의 값이 가장 낮은 상이 안정하다). 자유에너지 ΔG의 식(1.1)은 Devonshire가 부여한 자발분극(Pi)의 항, 식(1.2)은 인가 (Xi) 응력을 포함하는 항으로, 식(1.3)은 전기왜곡(Qij)을 결합계수로 한 응력과 자발분극의 협력항이다.

3. 유전율의 계산
유전 스티프니스(χij)는 식(1)에서 주어진 자유 에너지 ΔG의 2차 미계수로서 다음 식에서 주어진다.

정방정(Tetragonal), 사방정(Orthorhombic), 능면체정(Rhombohedral), 입방정(Cubic)의 각 결정상에 대응하는 유전스티프니스(χij)는 다음 식으로 주어진다.

단, 구해진는 비유전율(εij)은 유전 스테이프니스(χij)의 역행렬이다.

입방정은 퀴리점(Tc)보다 고온쪽에 있으므로 비유전율(εij)은 Curie-Weiss 법칙에 따라 다음 식으로 계산하였다.

단, C는 퀴리 상수, T는 온도, T0는 전이 온도를 나타낸다.
세라믹스의 유전율(εs)의 구하는 방법으로서 a축, b축, c축의 각 비유전율의 단순 평균, 대수 평균, 행렬 평균이 알려져 있다. 이번에는 실험 결과와 비교적 좋은 일치를 본 다음 식으로 주는 행렬 평균으로 구했다.

그림 3에 비유전율(εs)의 온도 의존성을 나타내었다. 그림 중 T2는 능면 체정에서 사방정으로의 전이 온도이고, T1는 사방정에서 정방정으로의 전이 온도이며, Tc는 비유전율이 최대가 되는 온도 퀴리점이다. 그림 중에 파선에서 유전율의 역수(1/εs)의 온도 의존성을 나타내었다. 온도축과의 교점은 T0(즉, 상변태온도)이며, 정방정에서 입방정의 전이온도 T0이다. 실험값과 비교하여 각 상전이 온도, 비유전율의 값 등 좋은 일치를 나타내고 있다.

실용 MLCC의 경우 응력과 전계가 인가되는 경우가 많다. 그림4에 일반적으로 탄성체에 응력(stress)이 가해진 경우의 응력 분포를 나타내었다. X1, X2, X3는 인장 응력이며, X4, X5, X6 은 전단 응력이다. BaTiO3 세라믹스에 인가되는 응력 분포는 다음과 같은 경우로 나눌 수 있다.

(a) 세라믹스의 경우
X1=X2=-X3 X3>0일 때는 인장응력
X3<0일 때는 압축응력
2축의 정응력과 1축의 역응력이므로 매크로적으로는 응력은 제로이다.
X4=X5=X6=0으로 전단 응력은 없다고 했다.
(b) 정수압의 경우
X1=X2=X3 X3>0일 때는 일반적인 정수압이 추가된 경우이다
X3<0일 때는 특수한 세라믹스 구조로 실현되어 있다
그림 5에 (a) 세라믹스의 경우에서 X3>0, 즉 c축 방향으로 인장 응력, a축과 b축 방향에는 압축 응력을 인가한 경우의 비유전율도 온도 특성을 나타내었다. 그림 중, 실선으로 나타낸 경우가 응력 0인 경우이고, 파선으로 나타낸 경우가 인가응력 X.3=30MPa 인가한 경우이다. 비유전율 값은 전온도 영역(결정 구조)에서 감소했다. 한편 그림 5 좌측 상단에 나타내듯이 퀴리점은 인가응력이 0MPa, 30MPa, 60MPa로 증대됨에 따라 고온측으로 이동하였다.

그림 6에 정사각정에서 입방정으로의 전이온도 Tc, 사방정에서 정사각정으로의 전이온도 T1, 능면체결정에서 사방결정으로의 전이온도 T2의 인가응력 의존성을 나타내었다. 응력 > 0인 경우는 c축에 인장 응력이 인가되어 있다. 반대로 응력<0인 경우는 c축에 압축응력이 인가되어 있다. T0의 응력 의존성은 4.0~4.5°C/100MPa였고 T1의 응력의존성은 4.5~6.0°C/100MPa, T2의 응력의존성은 -4.0~5.5°C/100MPa였다. 참고 문헌 10의 실험 결과를 설명할 수 있었다.

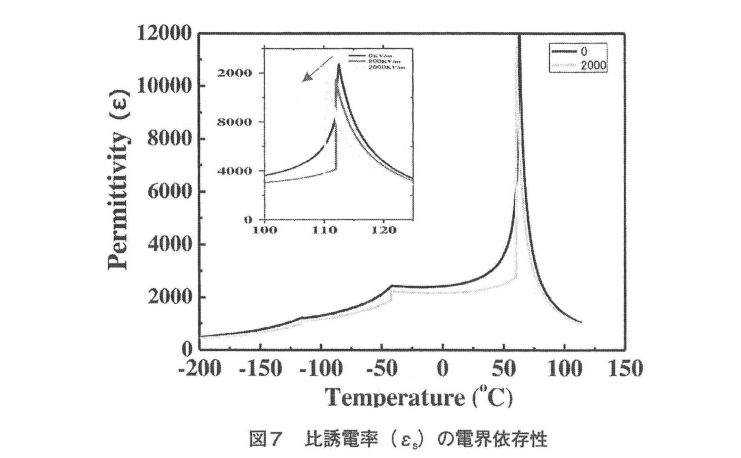
그림 7에 정전계를 인가한 경우의 비유전율의 변화를 나타내었다. 실선이 전계를 인가하지 않는 경우로 파선이 E=2,000V/m인 전계를 인가한 경우이다. 그림 7 왼쪽 상단에 큐리점의 변화를 나타내었다. 응력인가와 비교하면 변화량이 작다. 분극처리에서 알 수 있듯이, 전계인가의 경우, 도메인의 이동·회전이 발생한다.이 현상론적 열역학 계산에서는 도메인의 효과는 고려하지 않는다.
4. 격자정수의 계산
Devonshire의 현상론적 열역학에서는 자곡 에너지 ΔG가 자발분의 역급수로 나타낼 수 있음을 보여줬다. 격자상수는 자발분극(Ps)이 0이고 자발왜곡(Si)이 0인 단위격자(입방정)가 자발왜곡의 발생으로 어떻게 변화하는지를 고려함으로써 구해진다. 위의 과정으로부터 격자상수는 각 결정계에서 다음 식으로 주어진다.

그림 8에 계산 결과를 나타내었다. 실선이 인가응력 0인 경우이고, 파선이 인가응력 80MPa 인가인 경우이다. 고온의 입방정의 격자 상수 a, b, c축 모두 동일하게 ac에서 선팽창 계수를 따르고 있다. 입방정에서 정방정의 전이점 T0에서 c축과 a=b축으로 나뉘며(c축>a=b축), 그림에 나타난 것과 같은 변화를 나타낸다. 이어서 정사각정에서 사방정의 전이점 T1에서 c축 > a'=b'축으로 나뉜다. 더욱이, 사방정에서 능면체정의 전이점 T1에서 능면체정의 특징인 a축=b축=c축, 각 결정이 이루는 각도는 α=β=γ가 되고, a=arctan(Q44 P3^2)에 따라 변화한다. 그림 9에 자발 분극 P3의 온도에 의한 결정구조 의존성을 나타내었다. 이 자발 분극의 온도 의존성은 식(7)에서 부여한 각 결정 구조의 a, b, c축의 값에 크게 영향을 받는다

5. 결론
1991년 필자가 현상론적 열역학을 이용한 강유전체 특성 시뮬레이션을 시작한 것은 1985년 L.E.Cross 선생님의 방위대학 특강을 들은 것이 계기다. 당시, 나는 오카자키 키요시 교수의 밑에서 강유전체 세라믹스의 연구를 막 시작한 조수였다. 실험만 하던 나는 실험의 뒷받침이 계산으로 가능한 것에 충격을 받았다. 그 후, BaTiO3, PbTiO3의 단일 성분에서 PbTiO3-PbZrO3, PbTiO3-Pb(Zn1/3Nb2/3)O3의 2 성분계, PbTiO3PbZrO3Pb(Ni1/3Nb2/3)O3의 3 성분계의 특성 시뮬레이션을 실시했다. 현상론적 열역학은 위대하다!

'2020-적층세라믹콘덴서의 재료-제조-실장기술과 최신기술' 카테고리의 다른 글
| 제3장5절 저유전율계 재료 (0) | 2022.05.29 |
|---|---|
| 제3장4절 고유전율재료(Core-shell, Non core-shell) (0) | 2022.05.28 |
| 제3장2절 티탄산바륨의 그레인사이즈 효과 (0) | 2022.05.24 |
| 제3장1절 티탄산바륨의 유전분극기구 (0) | 2022.05.22 |
| 제2장 5절 특수한 단자전극 (0) | 2022.05.22 |